That's So Random
There's an old statistical legend (yes, we have legends) about a researcher who wanted to survey a sample of soldiers with a questionnaire about a particular topic. The researcher secured the cooperation of the Army, and the post commander provided a list of all the soldiers on the post. That was the sampling frame—the list from which survey subjects would be chosen. Based on the number of soldiers on the list, and the sample size the researcher desired, they figured that choosing 1/12th of the people on the list would be about right. So they started at the top and chose every 12th name to participate in the survey.
The problem was, this was the Army. The list was organized by company, platoon, squad, and so on. And that's how the names were listed, with the squad leader (typically a sergeant) listed at the head of their squad. And the squads consisted of 12 soldiers. So the researcher ended up with a sample containing only sergeants, and moreover only sergeants who were also squad leaders. So any results from surveying just these folks would clearly not be representative of the broader population of soldiers as a whole.
I don't know if this story is true, but it is certainly educational. It teaches us a lot about radomness and sampling. "Random" is a word used a lot in research and statistics But what does "random" really mean?
In a nutshell, "random" means patternless. Choosing every 12th name from a list is definitely a pattern, so it's not random. The survey of soldiers might have worked out OK if the names were not listed in any order or structure, but they were. Same thing can happen with spouses or household members, who in many databases and on many lists appear consecutively.
While concise, that definition still leaves a lot of ambiguity. We can expand on the concept of patternless in a bit more technical detail. Random means that of all possible outcomes for each research subject, each of those outcomes has a known and non-zero probability of occurring. A person might be chosen for the survey, or not. Any given phone number might be dialed, or not. A patient might be assigned to active drug, or they might get placebo. The problem with the selection method in the Army story is that by definition, only the 1st, 13th, 25th, etc name would be selected. The other soldiers had no chance of being selected for the survey.
Spatial point patterns are a good way to illustrate randomness. Figure figure 1 shows 8 points randomly located in a square space.
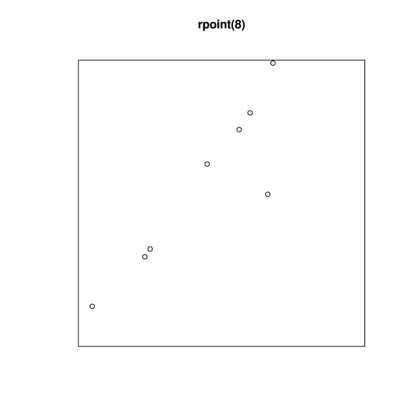
Figure 1: 8 points randomly located in a square
Now you might feel an urge to say, "Wait! Those 8 points aren't random. They're practically a straight line!" But that's randomness for you. I assure you my procedure (using the spatstat package in R) produces points randomly; each of the infinite number of spots in the square has some probability of getting, or not getting, inked. Here is the R command:
library(spatstat) plot(rpoints(8))
Now most times, a randomly-generated collection of 8 points in a square will not look straight-line-ish. But this time it did. Random does not mean an eye-pleasing, uniform spread. Randomness or randomization is a process, not any particular outcome.
Methods of randomization or random selection
So when designing a study, or appraising someone else's, that involves random selection or assignment, focus on the methods used to do the randomizing. Reasonable methods include:
- Flipping a coin
- Rolling dice
- Drawing a card from a deck of 52
- Using a computerized random number generator
Assigning subjects alternately to different treatments is convenient but is not random. It's a pattern. As soon as a subject is assigned to one treatment, the next subject in line has zero chance of being assigned to that same treatment. So not random.
An interesting example
Sometimes researchers feel they must accomodate what they see as operational realities. Here is an interesting study from the Houston, TX, EMS system, from 1994:
The team studied two different approaches to intravenous fluid resuscitation of injured patients in the field. The two methods were alternated, one day to the next. Everyone with qualifying injuries on a given day would receive one treatment. Everyone injured on the next day would receive the other treament. And so on, back and forth. This is not random assignment. The researchers state their case as to why they did it this way, and they make their argument that it was still satisfactory for drawing conclusions. The reader will have to decide for themselves. What do you think? I harbor some reservations, although they aren't necessarily show-stoppers. If nothing else, proceeding as they did would call for a different approach to the statistical analysis, which I may try to discuss in a future blog post.
Why this matters
Most statistical reasoning is based on the premise of randomness. Whether it's an interventional trial, an observational study, or a survey, we are inclined to accept the results in the study as representing truth in the universe if the subjects participating were assigned, observed, or chosen randomly, and thus accurately represent all the other similar subjects who were not chosen, or all the other ways the patients could have been assorted into the different treatments. If randomization was not properly done, the results should be questioned. Was randomization "properly done?" That depends on the procedures used in the study---usually found in the Methods section. It does not depend on the outcome of randomization or random selection, as might be described early in the Results section.
 Agency Statistical Consulting
Agency Statistical Consulting